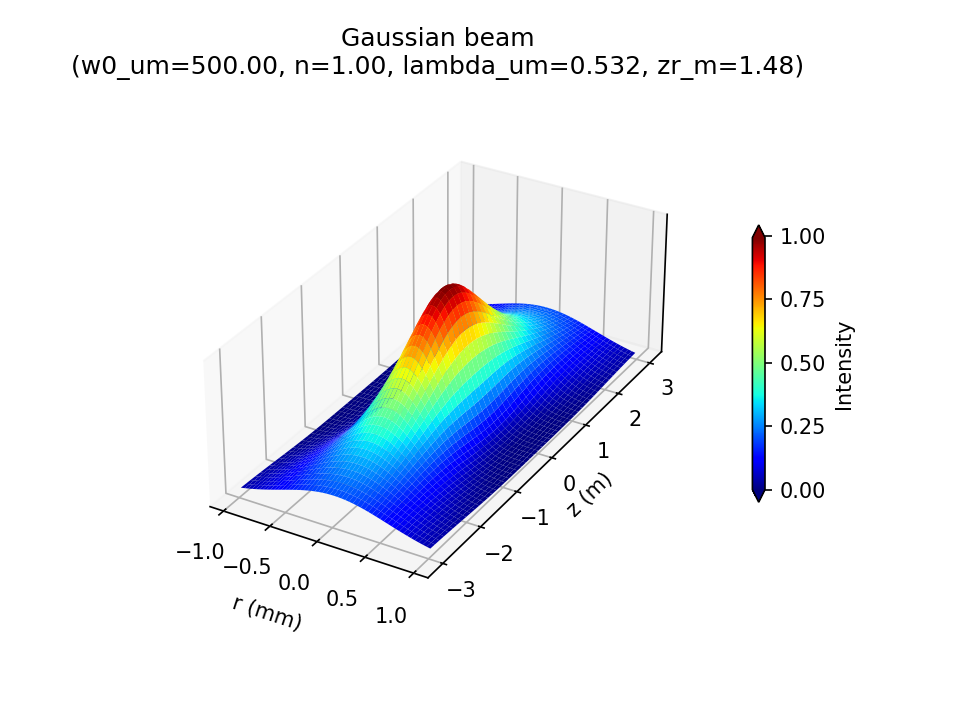
Gaussian beam

Contents

• Paraxial limit
• Rayleigh range
• Peak intensity
• Axial intensity
• Radial intensity
• Beam profile
• Beam divergence
• Numerical aperture
• Total power
• Power through aperture

Intensity equations

From Steck 2006, Mondal 2014 and Peatross 2015 the intensity \(I\) as a function of the beam radius \(r\) and axial displacement \(z\) is: \[ I(r,z) = I_0 \left(\frac{w_0}{w(z)}\right)^2 \exp \left(\frac{-2r^2}{w(z)^2}\right) \tag{1}\] where, \[w(z) = w_0\sqrt{1 + \left(\frac{z}{z_R}\right)^2} \tag{2}\] and \[z_R = \frac{\pi w_0^2 n}{\lambda_0} \tag{3}\] Here \(I_0\) is the peak intensity, \(w_0\) is the 'beam waist' (narrowest radius), \(n\) is the refractive index of the medium, \(\lambda_0\) is the vacuum wavelength and \(z_R\) is the 'Rayleigh range'.