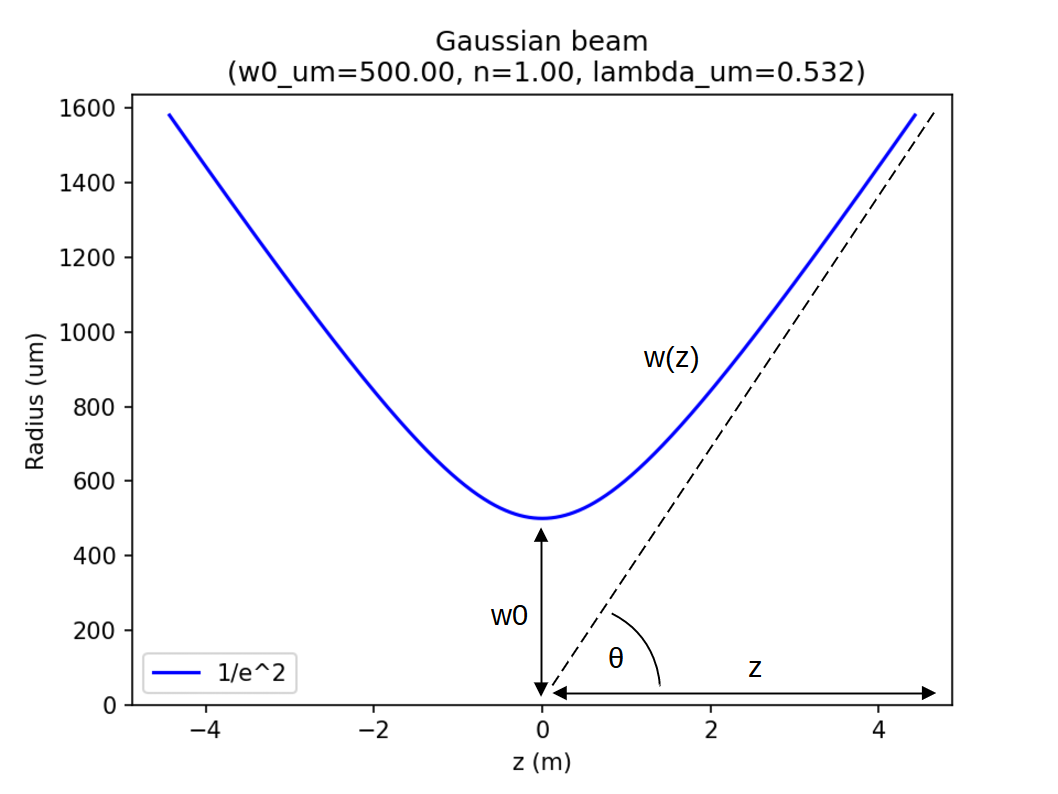
Gaussian beam

Beam divergence

From the definitions (1) and (2): \[w(z) = w_0\sqrt{1 + \left(\frac{z}{z_R}\right)^2} \tag{1}\] \[z_R = \frac{\pi w_0^2 n}{\lambda_0} \tag{2}\] Equation (1) is the 'one-over e squared' beam profile, which at large enough \(z\) tends towards a fixed 'divergence' angle \(\theta\): \[ \tan\theta = \lim_{z\to \infty} \left(\frac{w(z)}{z}\right) \tag{3}\] where: \[ \frac{w(z)}{z} = w_0 \sqrt{\frac{1}{z^2} + \frac{1}{z_R^2}} \tag{4}\] and so in the paraxial limit \(\tan\theta \approx \theta\): \[ \theta \approx \frac{w_0}{z_R} \tag{5}\]