Gaussian beam

Power through aperture

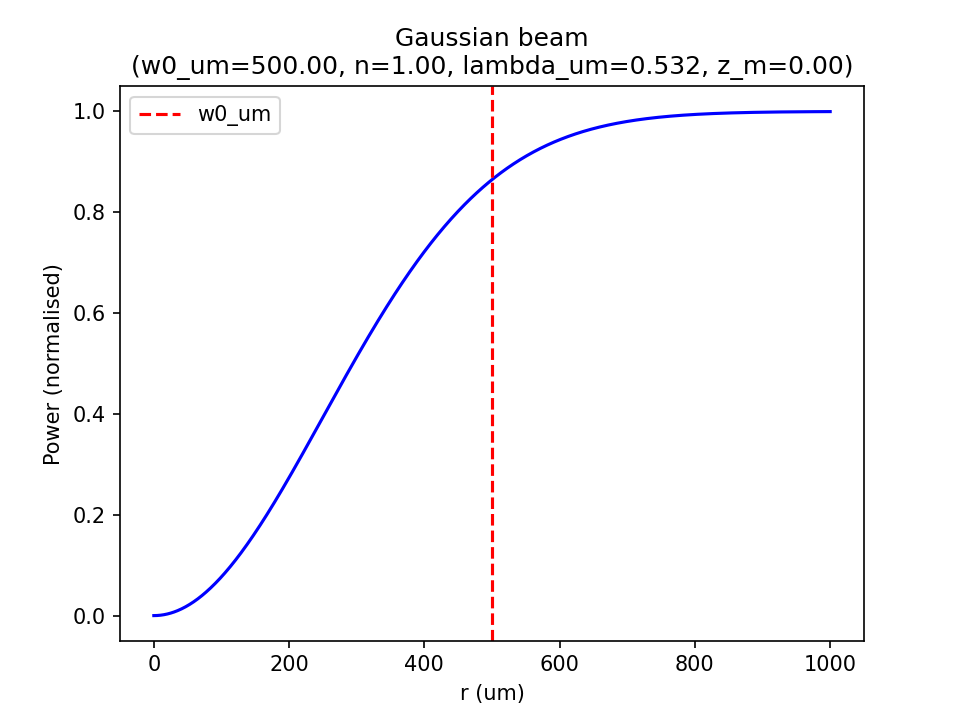
Following the same shell integration method as the 'total power' derivation, we can find the power as a function of \(r\) and \(z\) in a general form: \[ P(r,z) = 2\pi \int_0^r rI(r,z) dr \tag{1}\] where: \[ \int rI(r,z) dr = -\frac{1}{4}w(z)^2 I(r,z) \tag{2}\] and so: \[ P(r,z) = 2\pi \left[ -\frac{1}{4}w(z)^2 I(r,z) \right]_0^{r} \tag{3}\] and from the definition of \(I(r,z)\): \[ w(z)^2I(r,z) = I_0 w_0^2 \exp \left(\frac{-2r^2}{w(z)^2}\right) \tag{4}\] so we can rewrite (3) into: \[ P(r,z) = \frac{1}{2} \pi I_0 w_0^2 \left[ -\exp \left(\frac{-2r^2}{w(z)^2}\right) \right]_0^{r} \tag{5}\] and evalute to the convenient form: \[ P(r,z) = P_0 \left[1 - \exp \left(\frac{-2r^2}{w(z)^2}\right) \right] \tag{6}\] Note that if we set the apeture to radius to \(r=w(z)\) then we block about 13.5% of the light: \[ P(w(z),z) = P_0 \left[1 - \frac{1}{e^2} \right] \approx 0.86P_0 \tag{7}\]