Gaussian beam

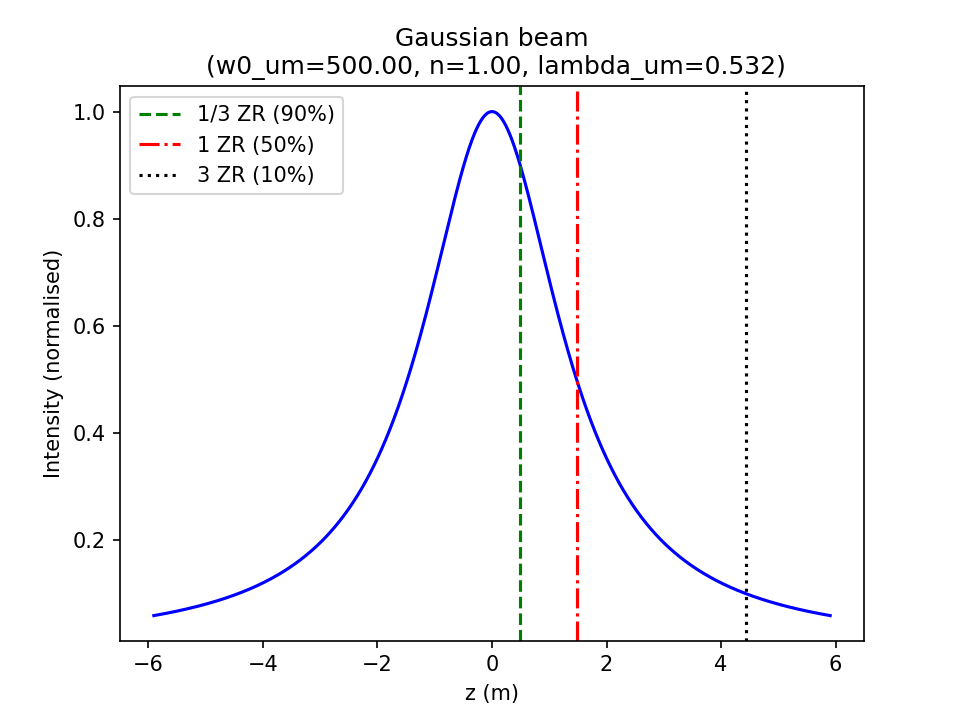
Axial Intensity

From the definitions (1) and (2): \[ I(r,z) = I_0 \left(\frac{w_0}{w(z)}\right)^2 \exp \left(\frac{-2r^2}{w(z)^2}\right) \tag{1}\] \[w(z) = w_0\sqrt{1 + \left(\frac{z}{z_R}\right)^2} \tag{2}\] for the axial intensity (\(r=0\)) we can write (1) as: \[ \frac{I(0,z)}{I_0} = \left(\frac{w_0}{w(z)}\right)^2 \tag{3}\] which simplifies to a Lorentzian profile: \[ \frac{I(0,z)}{I_0} = \frac{1}{1 + \left(\frac{z}{z_R}\right)^2} \tag{4}\] So at the Rayleigh range the intensity will half: \[ \frac{I(0,z_R)}{I_0} = \frac{1}{2} \tag{5}\] and therefore the 'full width half max' (FWHM) of a Gaussian beam, or the confocal parameter, is twice the Rayleigh range: \[ z_{FWHM} = 2z_R \tag{6}\] The 90% and 10% limits are found at \(z_R/3\) and \(3z_R\) (i.e beam lengths of \(2z_R/3\) and \(6z_R\)):