Gaussian beam

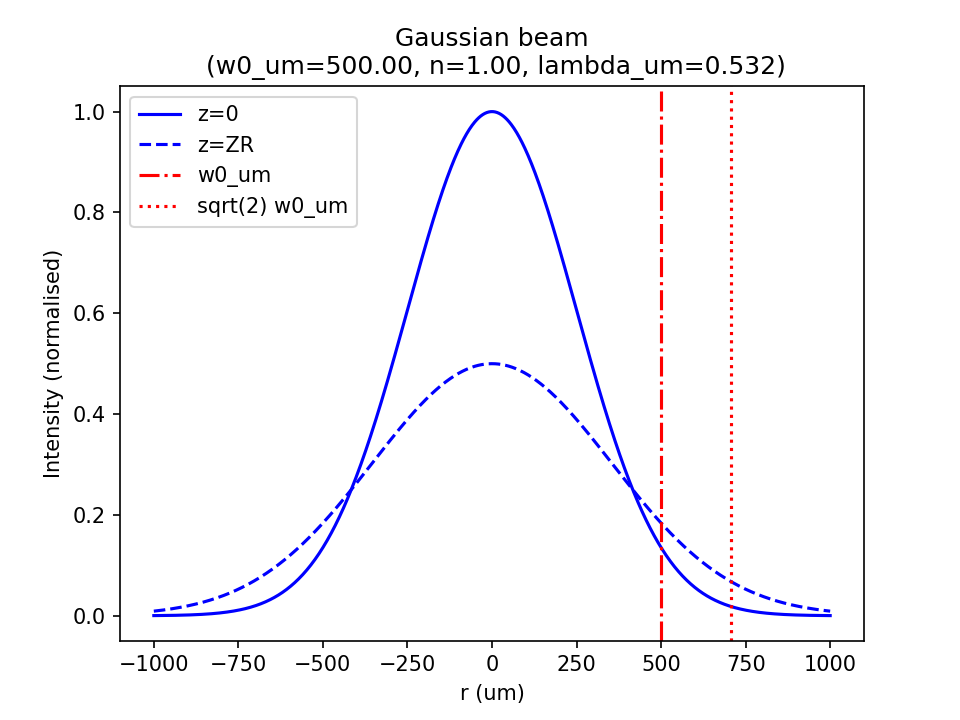
Radial Intensity

From the definitions (1) and (2): \[ I(r,z) = I_0 \left(\frac{w_0}{w(z)}\right)^2 \exp \left(\frac{-2r^2}{w(z)^2}\right) \tag{1}\] \[w(z) = w_0\sqrt{1 + \left(\frac{z}{z_R}\right)^2} \tag{2}\] we can see that in general, for any value of \(z\), the radial intensity follows a Gaussian profile (i.e. \(r\) exists only in the form of \( e^{-r^2} \)). So for example if we look at the beam waist \(z=0\): \[ \frac{I(r,0)}{I_0} = \exp \left(\frac{-2r^2}{w_0^2}\right) \tag{3}\] If we then pick \(r=w_0\), we see that \(w_0\) is the 'one-over e squared' radius, i.e. the distance at which the intensity has fallen to ~13.5%: \[ \frac{I(w_0,0)}{I_0} = \frac{1}{e^2} \tag{4}\] As an alternative example, we can look at the profile at the Rayleigh range: \[ \frac{I(r,z_R)}{I_0} = \frac{1}{2} \exp \left(\frac{-r^2}{w_0^2}\right) \tag{5}\] i.e. still a Gaussian, but with half the amplitude and √2 wider: