Gaussian beam

Beam profile

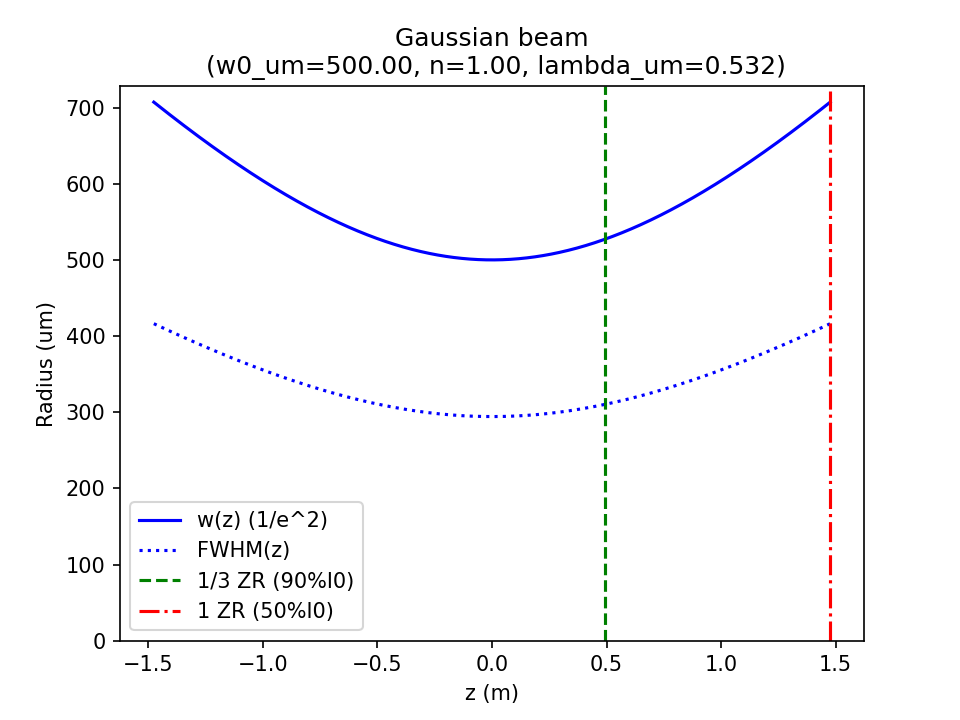
From the definitions (1) and (2): \[ I(r,z) = I_0 \left(\frac{w_0}{w(z)}\right)^2 \exp \left(\frac{-2r^2}{w(z)^2}\right) \tag{1}\] \[w(z) = w_0\sqrt{1 + \left(\frac{z}{z_R}\right)^2} \tag{2}\] if we set \(r=w(z)\), then: \[ I(w(z),z) = \frac{1}{e^2} I_0 \left(\frac{w_0}{w(z)}\right)^2 \tag{3}\] which we can re-write in terms of the axial intensity: \[ I(w(z),z) = \frac{1}{e^2} I(0,z) \tag{4}\] i.e. the radius \(r=w(z)\) traces out the axial intensity at the 'one-over e squared' limit (~13.5%), which we can consider the 'beam profile' as a function of \(z\).

Sometimes the 'full width half max' (FWHM) is more useful, which we can find by setting \(r=\frac{FWHM(z)}{2}\) in equation (4), and choosing the factor \(\frac{1}{2}\) (instead of \(\frac{1}{e^2}\)): \[ I(\frac{FWHM(z)}{2},z) = \frac{1}{2} I(0,z) \tag{5}\] So by comparing (5) to (1), we see that the exponential term should match the 'half', which gives: \[ \exp \left(\frac{-2(\frac{FWHM(z)}{2})^2}{w(z)^2}\right) = \frac{1}{2} \tag{6}\] taking the natural log leads to: \[ -\frac{1}{2} \left(\frac{FWHM(z)}{w(z)}\right)^2 = \ln1 - \ln2 \tag{7}\] which simplifies to a factor of ~1.18: \[ FWHM(z) = \sqrt{2\ln2} \; w(z) \tag{8}\] A similar derivation can be done for the 90% limit giving a factor of ~0.46: \[ FW90M(z) = \sqrt{2\ln(10/9)} \; w(z) \tag{8}\]