Gaussian beam

Paraxial limit

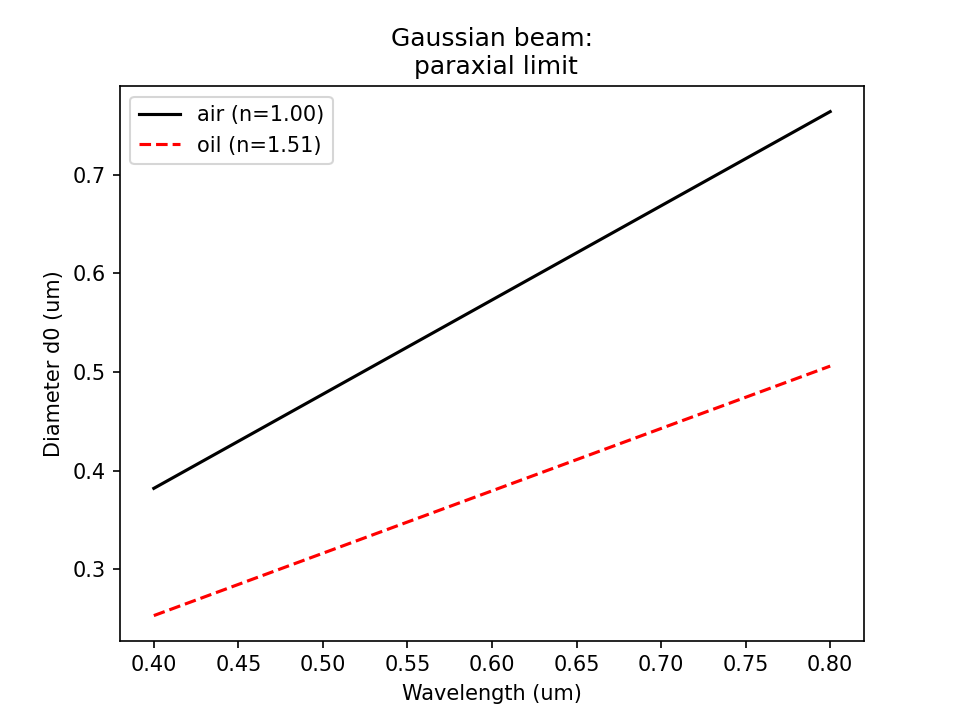
From Vaveliuk 2007 the paraxiality estimator \(\tilde{P}\) for a Gaussian beam \((N=0)\) is: \[ \tilde{P} = 1 - 1/\tilde{k}^2 \tag{1}\] where: \[ \tilde{k} = kw_0 = \frac{2 \pi w_0}{\lambda} \tag{2}\] They suggest in the main text (and Fig. 1.) that it is reasonable to take: \[ \tilde{P} \geq 0.88 \tag{3}\] So we can rewrite (1) with \(0.88 \approx 8/9\): \[ 1 - 1/\tilde{k}^2 \geq 8/9 \tag{4}\] which reduces to: \[ 1/3 \geq 1/\tilde{k} \tag{5}\] or more conveniently: \[ \frac{2 \pi w_0}{\lambda} \geq 3 \tag{6}\] substituting in the vacuum wavelength \(\lambda_0(=n\lambda)\) and rearranging gives: \[ w_0 \geq \frac{3 \lambda_0}{2 \pi n} \tag{7}\] or in terms of the beam diameter \(d_0(=2 w_0)\) and the appoximation \(3/\pi \sim 1\): \[ d_0 \geq \frac{\lambda_0}{n} \tag{8}\]