Microscope objectives

Optical pixels

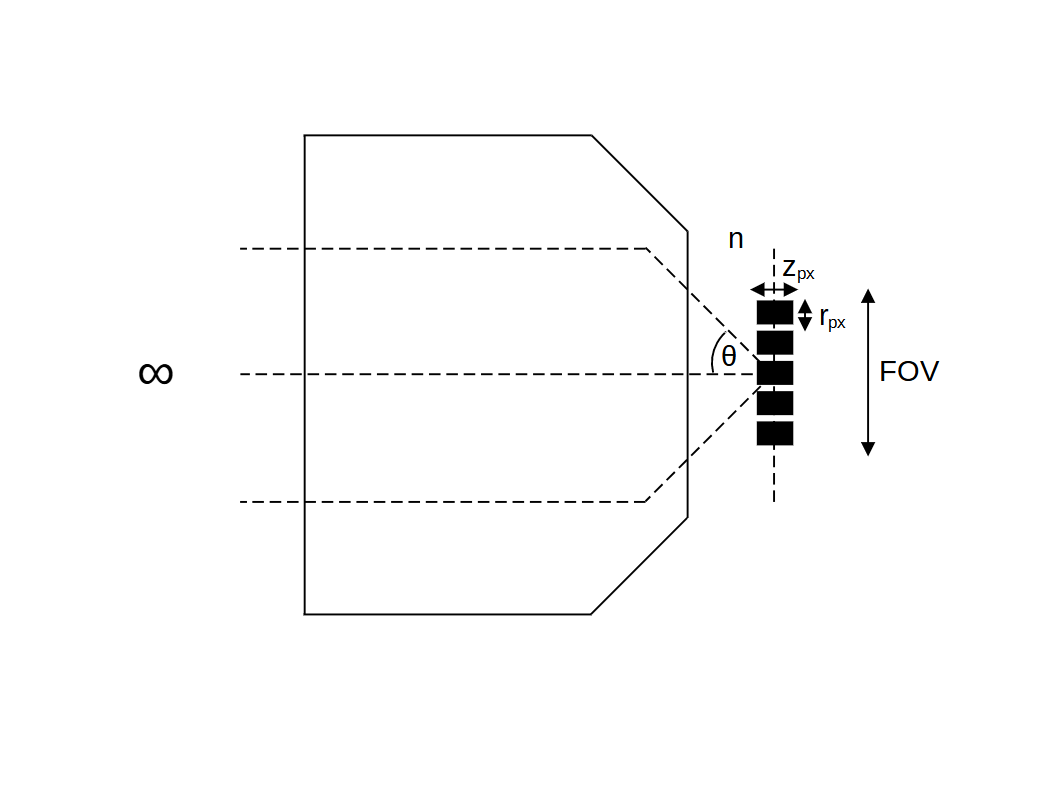
According to the Nyquist criterion (Pawley 2006), the interval between intensity measurements (the pixel size) should be less than or equal to half the smallest feature size: \[ r_{px} \leq \frac{1}{2} r_{min} \tag{1}\] and, \[ z_{px} \leq \frac{1}{2} z_{min} \tag{2}\] If the smallest features are sub-diffractive, then (in a traditional imaging regime) we can use the expected size of the diffraction limited point spread function to determine the correct pixel size: \[ r_{px} \leq \frac{1}{2} \frac{0.61 \lambda_0}{NA} \tag{3}\] and, \[ z_{px} \leq \frac{n \lambda_0}{NA^2} \tag{4}\] In this case, the voxel aspect ratio scales with the collection half angle according to: \[ \frac{z_{px}}{r_{px}} = \frac{3.28}{\sin\theta} \tag{5}\] For most objectives \( 0.1 \leq \sin\theta \leq 0.95 \), and so in this regime the axial pixels are significantly longer than the radial pixels: \[ 3.5 \leq \frac{z_{px}}{r_{px}} \leq 32.8 \] When considering optics and camera chips it is often useful to calculate the number of pixels in the field of view: \[ N_{px} = \frac{FOV}{r_{px}} \tag{6}\]