Microscope objectives

Infinity correction

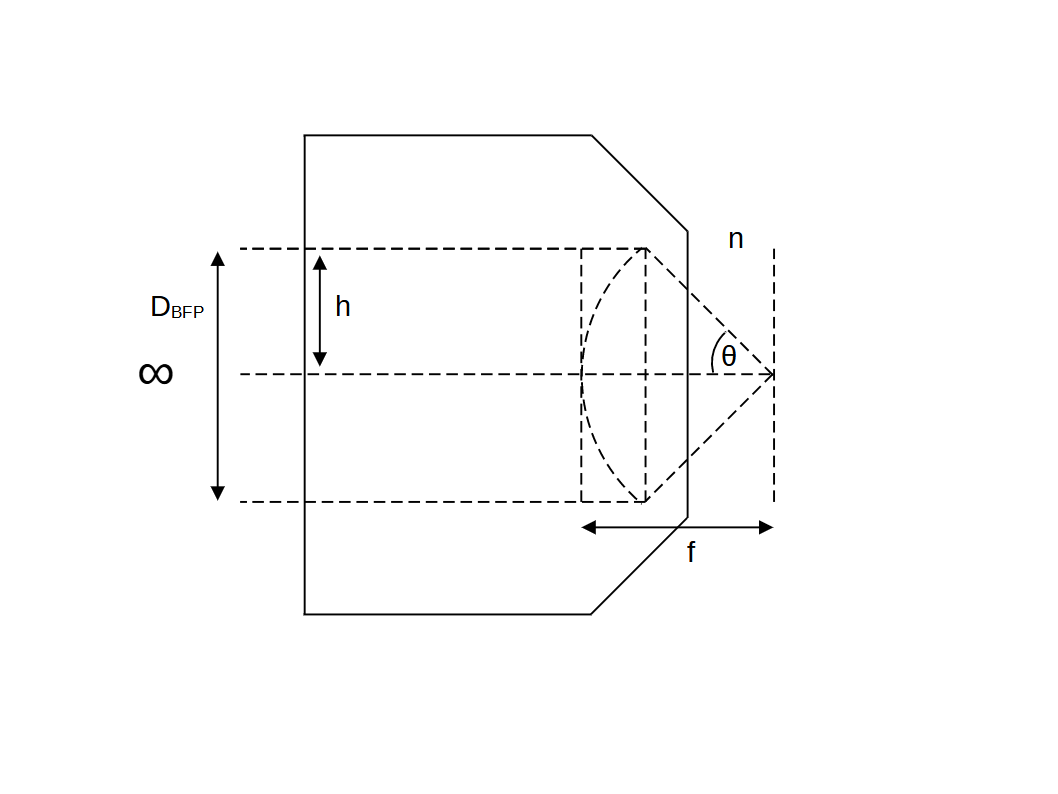
An ideal infinity corrected objective can collect the emission from a point particle at the specified \(NA\) (i.e. a portion of a spherical wave) and produce a plane wave at the back aperture. So in other words, an object plane (P_o below) is 'sent' to an image plane (P_i below) at an infinite distance, which is a key property we can use to determine how the lens operates (even if we don't know what's inside).

From Hecht 2016, an optical system which images off-axis points (like p_o1 to p_i1) at high angular aperture (e.g. a high \(NA\) microscope objective) must obey the sine condition: \[ y_i n_i \sin\gamma_i = y_o n_o \sin\gamma_o \tag{1}\] where \(y\) is the height of the point from the optic axis, \(\gamma\) is the angle the marginal ray makes with the optic axis and \(n\) is the refractive index of the medium (and subscripts 'o' and 'i' are for object and image space):

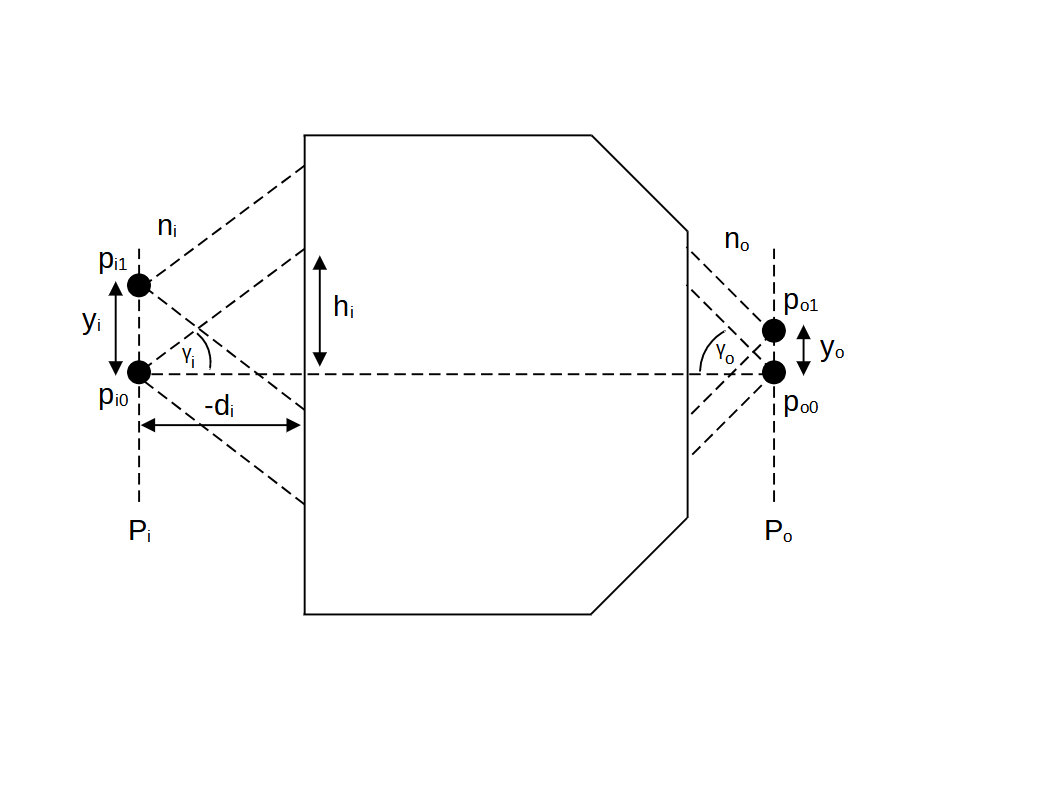
From Born 2019, if we now consider a pair of points on the optic axis (p_o0 and p_i0), and 'send' the image plane (P_i) very far to the left by a distance \(-d_i\) (i.e. towards \(-\infty\)) then we can see that as the angle gets small \(\sin\gamma_i \to \gamma_i\), and we can write: \[ \gamma_i = \lim_{d_i\to \infty} \left(\frac{h_i}{-d_i}\right) \tag{2}\] So in the limit of infinity corrected objectives, we can rewrite (1) as: \[ y_i n_i \left(\frac{h_i}{-d_i}\right) = y_o n_o \sin\gamma_o \tag{3}\] From the paraxial solutions to geometrical optics, (now valid on the left since \(\sin\gamma_i \to \gamma_i\)) we can use the relations for the lateral magnification \(M_T\): \[ M_T = \frac{y_i}{y_o} = -\frac{d_i}{f_i} \tag{4}\] Combining (3) and (4) simplifies to: \[ n_i \left(\frac{h_i}{f_i}\right) = n_o \sin\gamma_o \tag{5}\] Since the image is normally formed in air (\(n_i=1\)), we can set \(\gamma_0 = \theta\) and drop the subscripts to write: \[ h = f n \sin\theta \tag{6}\] which produces the familiar equation for the diameter of the back focal plane \(D_{BFP}\) (Gross 2008): \[ D_{BFP} = 2 f NA \tag{7}\] Note: equation (6) has important implications for how we use an infinity corrected objective. The 'rays' from the object map to the exit pupil according to \(\sin\theta\), so the pupil is not a plane, but a spherical cap: