Microscope objectives

Immersion

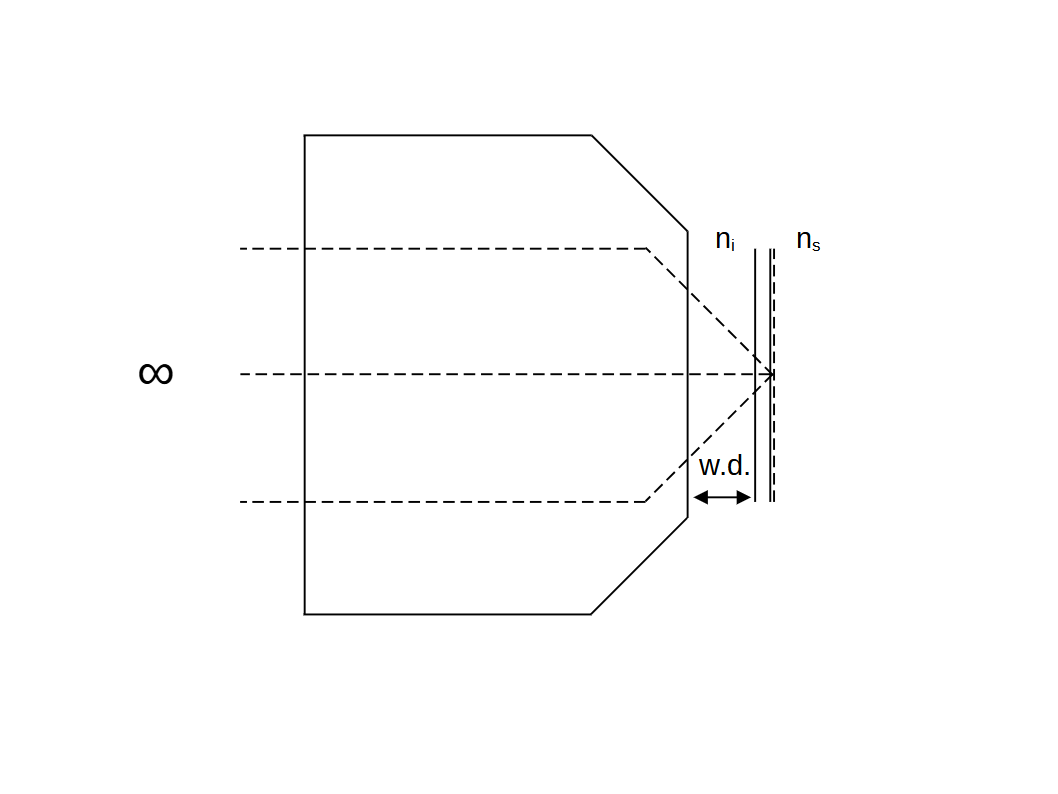
The space between the front of an objective and the image plane is an important part of the system, where the shape and refractive index matter. So objectives are designed to account for this space, and 'expect' an immersion medium of known refractive index \(n_i\) (and sometimes a coverslip of very particular specification). Filling the space with a substantially different refractive index (or coverslip) causes spherical aberration and produces blurry images at high numerical aperture (Pawley 2006).

When imaging a sample of refractive index \(n_s\) beyond the depth 'zero' image plane (i.e. focusing into the sample at some finite depth), slabs of immersion (with the correct refractive index) are effectively exchanged for slabs of sample. If the sample and immersion are refractive index matched then this is a 'null' operation and the objective will image as designed. However, if the sample and immersion refractive index are substantially different, then the images get blurrier with depth. So, in general, we require the condition: \[n_i = n_s \tag{1}\]

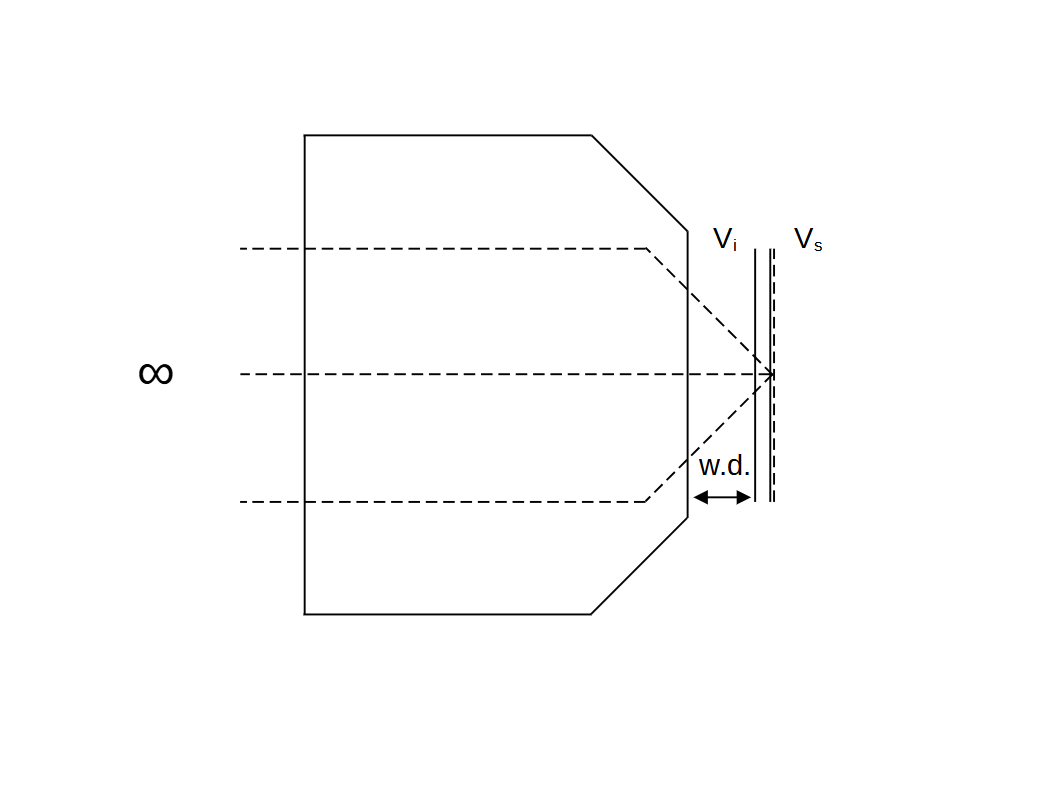
Similarly, the change in refractive index with wavelength is important for color correction, i.e the dispersion. The lens design 'expects' a particular dispersion, for example that of water or a particular oil. Dispersion is often (approximately) quantified with the Abbe number \(V_d\): \[V_d = \frac{n_d - 1}{n_F - n_C} \tag{2}\] where \(n_d\), \(n_F\) and \(n_C\) correspond to the refractive indices at the Fraunhofer lines at 587.56nm (yellow), 486.13nm (blue) and 656.28nm (red) respectively (Hecht 2016). So lower values of \(V_d\) are more dispersive and higher values are less dispersive. So, in general, we require that the dispersion of the immersion \(V_i\) and that of the sample \(V_s\) are equal: \[V_i = V_s \tag{3}\]