Microscope objectives

Focal length

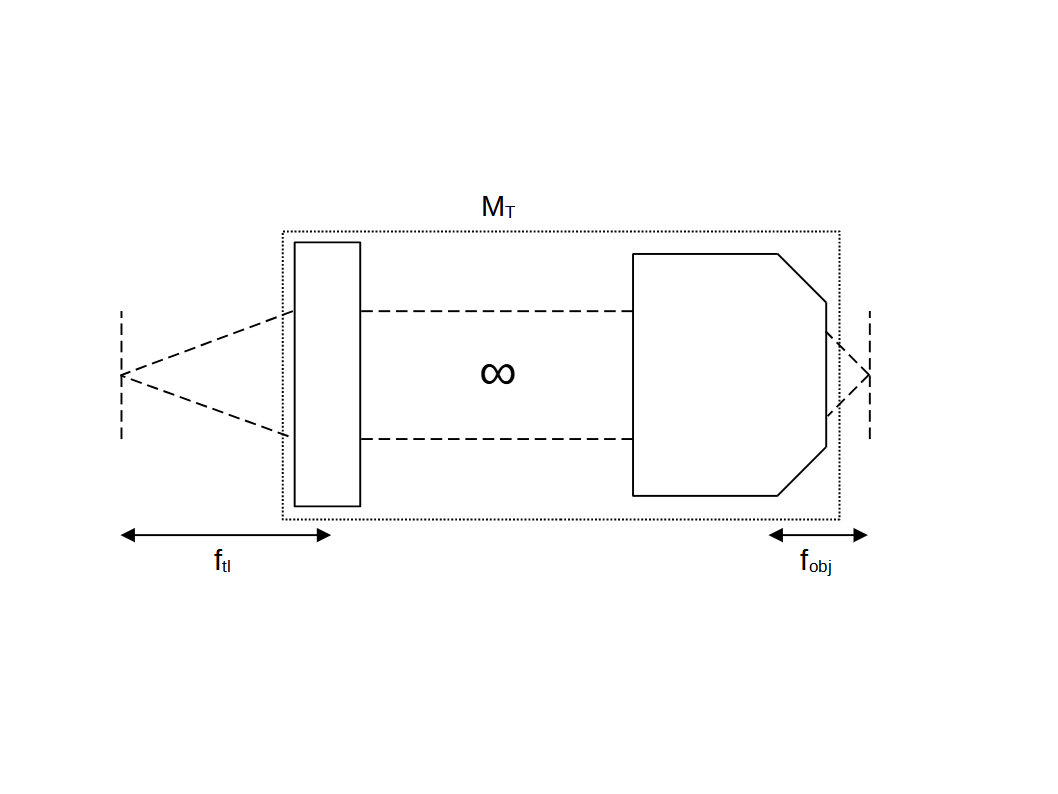
From Hecht 2016, in general the transverse magnification \(M_T\) is given by the ratio of the object and image distances (\(s_o\) and \(s_i\)) according to: \[ M_T = - \frac{s_i}{s_o} \tag{1}\] In the special case of an infinity corrected objective and tube lens pair, the object and image distances are equal to their focal lengths (\(f_{obj}\) and \(f_{tl}\)). So we can rewrite (1) in the more convenient form: \[ M_T = - \frac{f_{tl}}{f_{obj}} \tag{2}\] In (1) and (2) the negative sign is by convention, and just like the traditional equation for transverse magnification (\(M_T = - \frac{y_i}{y_o}\)) indicates an inverted image. We can therefore infer the focal length of the objective by rewriting (2) in the form: \[ f_{obj} = \frac{f_{tl}}{\vert M_T \vert} \tag{3}\] Note: the focal length (unlike the magnification) is a fundamental property of the objective. The magnification can now be adjusted by choosing tube lenses with different focal lengths (a useful degree of freedom for building instruments).