Microscope objectives
An introduction to 'infinity' corrected microscope objectives.
ContentsColor correction
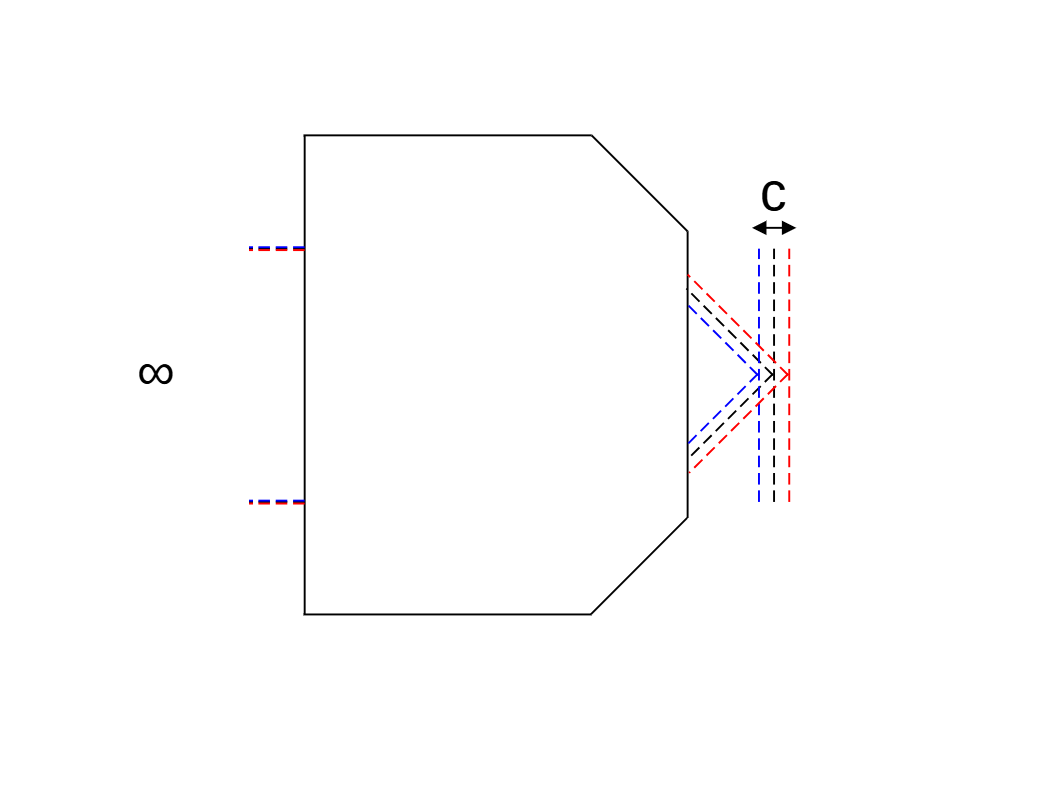
An ideal objective would image all wavelengths to the same point, and therefore be fully 'color' corrected. In practice the lens design has to battle the dispersive properties of the many glass elements that typically make up the objective, giving good performance only over a limited range. From Zhang 2019, the degree of color correction has historically been approximately classified according to the following table, which refers to the traditional depth of field: \[ DOF = \frac{n\lambda}{NA^2} \tag{1}\] where \(\lambda\) is the central wavelength. In the table and diagram below, \(C\) refers to the longitudinal chromatic abberation.
| Correction | With plan | Colors | Wavelength (nm) | C |
|---|---|---|---|---|
| Achromate | Plan-Ach | 2: RB | 486 - 656 | < 2.0xDOF |
| Fluorite | Plan-Fluor | 3: RGB | 436 - 656 | < 2.5xDOF |
| Apochromate | Plan-Apo | 3: RGB | 436 - 656 | < 1.0xDOF |
| VIS Apochromate | ≥ 3 | 404 - 768/852 | ||
| IR SuperApochromate | ≥ 3 | 404 - 1014 | ||
| UV Superapochromate | ≥ 3 | 365 - 656 | ||
| UV-IR Superapochromate | ≥ 3 | 365 - 852/1014 |