SOLS transmission

Spherical cap intersection

Numerical estimate

Andrew G. York wrote a nice Python script to numerically estimate the intersection of spherical caps with visualization , see it here.

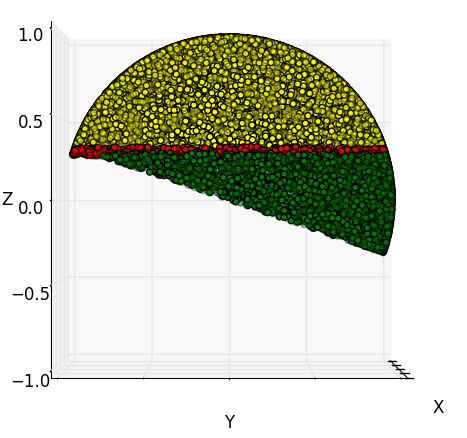
Analytical solution

DKR posted a detailed discussion on the analytical solution to calculate the area on a sphere of the intersection of two spherical caps \(A_n\) which is presented here: \[A_n = 2 r^2 (\pi - A\cos b - B \cos a - C) \tag{1}\] where: \[A = 2 \arctan \left ( \frac{k}{\sin(s - a)} \right ) \tag{2}\] \[B = 2 \arctan \left ( \frac{k}{\sin(s - b)} \right ) \tag{3}\] \[C = 2 \arctan \left ( \frac{k}{\sin(s - c)} \right ) \tag{4}\] \[k = \sqrt{\frac{\sin(s - a)\sin(s - b)\sin(s - c)}{\sin s}} \tag{5}\] \[s = \frac{1}{2}(a + b + c) \tag{6}\] and in the language of SOLS transmission \(a = \theta_2\) is the half angle of spherical cap 2, \(b = \theta_3\) is the half angle of spherical cap 3 and \(c = \theta_t\) is the tilt angle between the caps (\(r\) is radius for absolute calculations).

The area of spherical cap 2 \(A_2\) is simply: \[A_2 = 2 \pi r^2 (1 - \cos a) \tag{7}\] and so the fraction of transmitted rays between caps 2 and 3 is: \[T_3 = \frac{A_n}{A_2} \tag{8}\] or explicitly: \[T_3 = \frac{(\pi - A\cos b - B \cos a - C)}{\pi (1 - \cos a)} \tag{9}\]

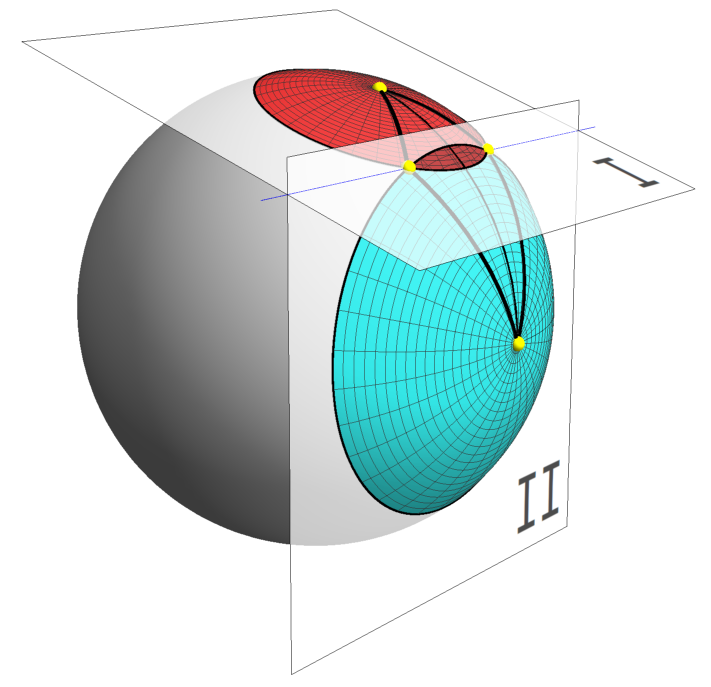
Comparison

The numerical solution typically converges to the analytical solution to within 1% if at least 1 million random points are used. Run this Python script to compare.