SOLS excitation

Light-sheet vs tilt

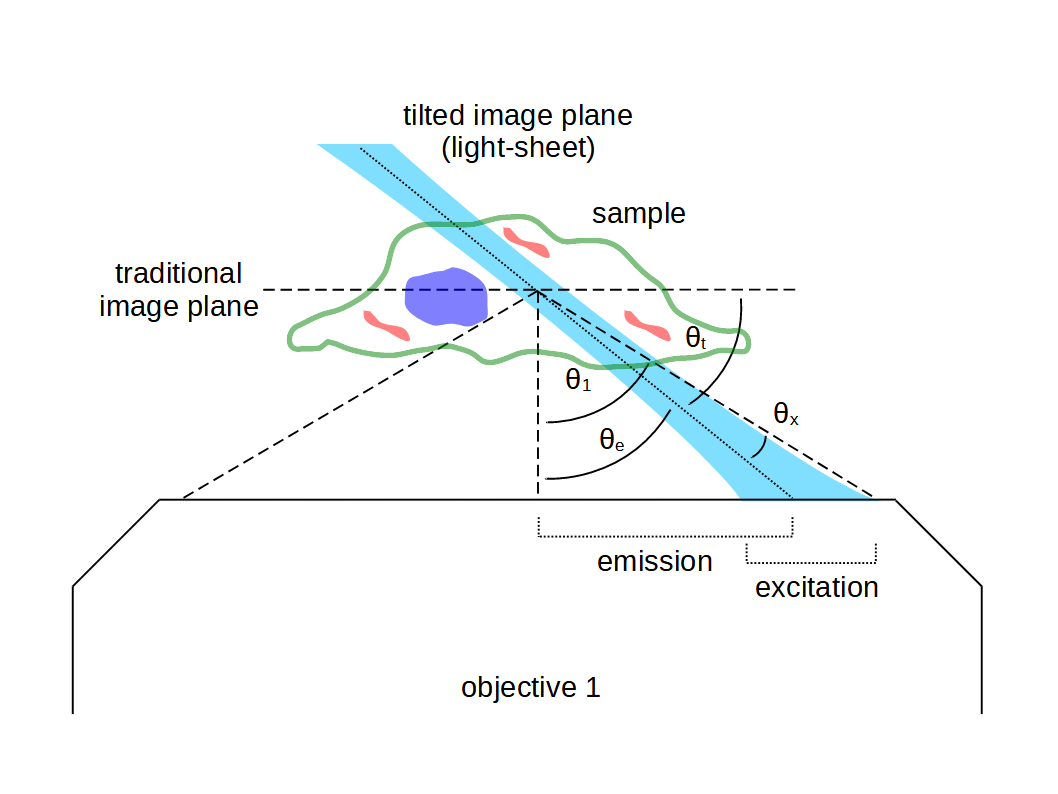
The SOLS architecture limits the light-sheet divergence \(\theta_x\) to: \[ \theta_x = \theta_1 - \theta_e \tag{1}\] where \(\theta_1\) is the collection half angle of the objective and \(\theta_e\) is the collection half angle of the emission (one side only). The emission half angle \(\theta_e\) is then related to the tilt of the 3rd microscope \(\theta_t\) according to: \[ \theta_e = \frac{\pi}{2} - \theta_t \tag{2}\] So, combining (1) and (2), we can see that for a given primary objective lens and tilt angle: \[ \theta_x = \theta_1 + \theta_t - \frac{\pi}{2} \tag{3}\] If we assume a Gaussian beam, then the thinnest light-sheet we can accommodate has a waist: \[ w_0 = \frac{\lambda_0}{\pi \theta_x n} \tag{4}\] i.e. more tilting allows thinner light-sheets, but reduces the collection on the emission path (one side only). The Rayleigh range is then related to the divergence with: \[ z_R = \frac{\lambda_0}{\pi \theta_x^2 n} \tag{4}\] i.e. thinner light-sheets have a much shorter range (since \(w_0 \propto \frac{1}{\theta_x}\) and \(z_R \propto \frac{1}{\theta_x^2}\)).